Algorithms, Pseudocode & Flowcharts

Topic: Problem-solving techniques using algorithms, pseudocode, and flowcharts

Course: C Programming Fundamentals

📚 Lecture Details

Prepared by: Dr. Mohsin F. Dar

Designation: Assistant Professor, School of Computer Science

Institution: UPES, Dehradun

Target Audience: B.Tech-CSE-I-B47 and B.Tech-CSE-I-B48

🎯 Learning Objectives

By the end of this lecture, students will be able to:

Understand the concept and importance of algorithms in problem-solving
Write clear and structured pseudocode for various problems
Create flowcharts using standard symbols and conventions
Compare and choose appropriate problem-solving methods
Apply these techniques to solve real-world programming problems
Analyze the efficiency and clarity of different approaches

🔍 What is an Algorithm?

Definition: An algorithm is a step-by-step procedure or set of rules designed to solve a specific problem or perform a particular task.

Key Characteristics of Algorithms:

🎯 Well-defined

Each step must be clear and unambiguous

📥 Input

Takes zero or more inputs

📤 Output

Produces at least one output

⏰ Finite

Must terminate after finite steps

✅ Effective

Each step must be feasible and executable

🔄 Deterministic

Same input produces same output

📝 Algorithm Example: Finding Maximum of Three Numbers

Problem: Find the largest among three numbers

Algorithm Steps:

START
INPUT: Read three numbers A, B, and C
INITIALIZE: Set MAX = A
COMPARE: If B > MAX, then set MAX = B
COMPARE: If C > MAX, then set MAX = C
OUTPUT: Display MAX as the largest number
STOP

🔍 Analysis:

Input: Three numbers (A, B, C)
Output: Maximum value among the three
Steps: 7 clear, executable steps
Efficiency: O(1) - constant time

📋 What is Pseudocode?

Definition: Pseudocode is a high-level description of a computer program's logic that uses natural language mixed with programming constructs.

Advantages of Pseudocode:

Language Independent: Not tied to any specific programming language
Easy to Understand: Uses natural language constructs
Quick to Write: Faster than actual code development
Easy to Modify: Changes can be made quickly
Bridge: Connects problem analysis to code implementation

Common Pseudocode Conventions:

BEGIN / START          - Start of algorithm
END / STOP            - End of algorithm
INPUT / READ          - Input operation
OUTPUT / PRINT        - Output operation
SET / ASSIGN          - Assignment operation
IF...THEN...ELSE      - Conditional statements
WHILE...DO            - Loop statements
FOR...TO...DO         - Loop statements
REPEAT...UNTIL        - Loop statements

📝 Pseudocode Example: Same Problem

Problem: Find the largest among three numbers

BEGIN FindMaximum
    INPUT A, B, C
    SET MAX = A
    
    IF B > MAX THEN
        SET MAX = B
    END IF
    
    IF C > MAX THEN
        SET MAX = C
    END IF
    
    OUTPUT "The maximum number is: ", MAX
END FindMaximum

🎯 Benefits:

Clear structure and logic
Easy to convert to any language
Readable by non-programmers

🔄 Translation to C:

This pseudocode can be easily translated to C, Python, Java, or any other programming language.

📊 What are Flowcharts?

Definition: A flowchart is a graphical representation of an algorithm that uses standard symbols to represent different types of operations and the flow of control.

Standard Flowchart Symbols:

START / STOP

Oval: Start and End points

PROCESS

Rectangle: Process / Action steps

DECISION

Diamond: Decision / Condition

INPUT / OUTPUT

Parallelogram: Input / Output operations

A

Circle: Connector (jumps to another part of flow)

DOCUMENT

Curved Rectangle: Document / Report

SUBPROCESS

Double-Rectangle: Predefined process / Subroutine

Flow Direction:

Arrows indicate the direction of flow. Example: START → PROCESS → DECISION? → YES/NO paths

📊 Flowchart Example: Finding Maximum

Problem: Find the largest among three numbers

START

↓

INPUT A, B, C

↓

MAX = A

↓

B > MAX?

YES: MAX = B NO: Skip

↓

C > MAX?

YES: MAX = C NO: Skip

↓

OUTPUT MAX

↓

STOP

🔄 Comprehensive Example: Sum of First N Natural Numbers

📝 Algorithm

START
INPUT N
SET SUM = 0
SET I = 1
WHILE I ≤ N DO
SUM = SUM + I
I = I + 1
END WHILE
OUTPUT SUM
STOP

📋 Pseudocode

BEGIN SumNaturalNumbers
    INPUT N
    SET SUM = 0
    SET I = 1
    
    WHILE I <= N DO
        SET SUM = SUM + I
        SET I = I + 1
    END WHILE
    
    OUTPUT "Sum is: ", SUM
END SumNaturalNumbers

📊 Flowchart: Sum of First N Natural Numbers

Flowchart for Sum of First N Natural Numbers

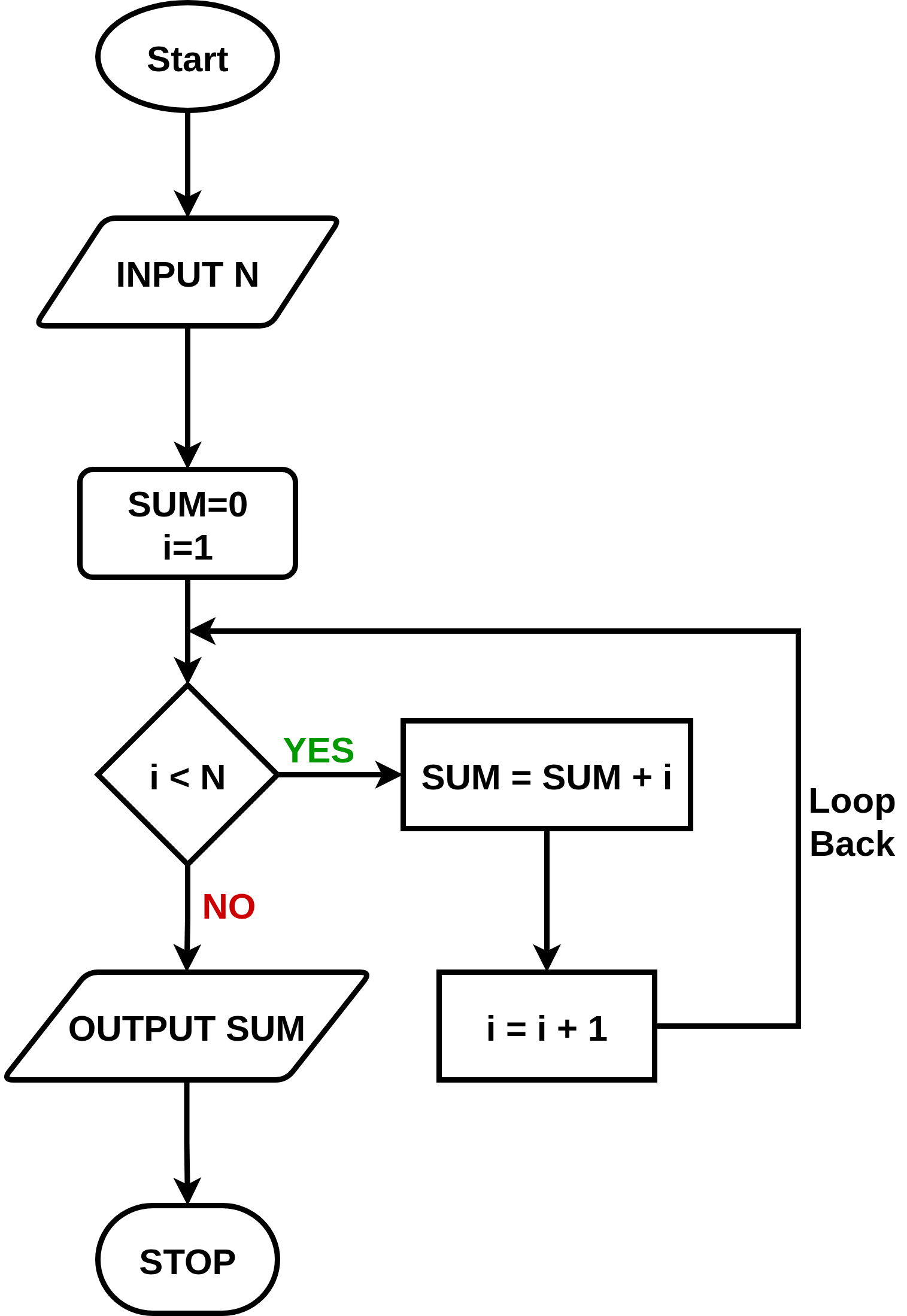
📝 Example Trace (N = 5):

Iteration 1: I=1, SUM=0+1=1
Iteration 2: I=2, SUM=1+2=3
Iteration 3: I=3, SUM=3+3=6
Iteration 4: I=4, SUM=6+4=10
Iteration 5: I=5, SUM=10+5=15
Final: I=6 > N=5, so OUTPUT SUM = 15

⚖️ Comparison: Algorithm vs Pseudocode vs Flowchart

Aspect	Algorithm	Pseudocode	Flowchart
Format	Step-by-step text	Structured text with keywords	Graphical symbols
Ease of Understanding	Good for logical thinkers	Easy for programmers	Visual, easy for everyone
Detail Level	High-level overview	Medium detail	Visual flow representation
Modification	Easy to modify	Very easy to modify	Requires redrawing
Space Required	Compact	Compact	More space needed
Best For	Problem analysis	Code planning	Visual communication

🎯 When to Use Each Method?

📝 Use Algorithms When:

Initial problem analysis
Documenting solution approach
Communicating with non-technical stakeholders
Breaking down complex problems
Academic or theoretical discussions

📋 Use Pseudocode When:

Planning code structure
Team collaboration
Code reviews and discussions
Language-independent design
Teaching programming concepts

📊 Use Flowcharts When:

Visual learners in audience
Complex decision structures
Process documentation
System design presentations
Debugging logic flow

Best Practice: Use all three methods complementarily! Start with an algorithm for problem understanding, create pseudocode for implementation planning, and draw flowcharts for visual verification and communication.

💪 Practice Problems

🎯 Try These Problems Using All Three Methods:

Problem 1: Basic

Calculate the factorial of a number

Input: A positive integer N

Output: N! (N factorial)

Problem 2: Intermediate

Check if a number is prime

Input: A positive integer N

Output: "Prime" or "Not Prime"

Problem 3: Advanced

Sort an array using bubble sort

Input: Array of integers

Output: Sorted array in ascending order

Assignment: For each problem, create:

A detailed algorithm with numbered steps
Structured pseudocode with proper keywords
A complete flowchart with standard symbols

📚 Summary

                Key Takeaways:
                Algorithms provide step-by-step problem-solving procedures
Pseudocode bridges the gap between algorithms and actual code
Flowcharts offer visual representation of program logic
Each method has its strengths and appropriate use cases
Practice with all three methods improves problem-solving skills

            

🎯 Next Steps:

Practice the assigned problems
Start with simple problems and gradually increase complexity
Compare your solutions with classmates
Begin implementing pseudocode in C programming

📖 Remember:

Think before you code
Plan your solution approach
Use the method that best fits your audience
Practice makes perfect!